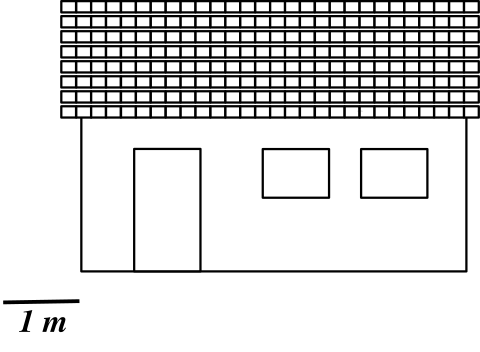
Correction 1

On mesure la longueur de l'échelle sur le plan qui correspond ici, dans la réalité à $1m$.

Ensuite, on mesure sur le plan la longueur au sol de la maison, puis on réalise "un produit en croix"

$$\table \bo \text"plan" , \bo \text"réalité"; 7mm , 1m ;35mm, x; $$

et donc

$$ x = {1m × 35mm} / {7mm} = 5.0 m$$

On trouve alors que la longueur de la maison est de $5.0m$ environ.

Correction 2

On mesure sur le dessin la distance entre l'origine et le repère $0.50m$. On trouve par exemple $32mm$, mais attention, cela dépend de la taille de l'écran.

On mesure ensuite la distance entre l'origine et $x$, on trouve par exemple $7.5mm$. On effectue un produit en croix.

$$\table \bo \text"plan" , \bo \text"réalité"; 32mm , 0.5m ;7.5mm, x; $$ $$ x = {0.5m × 7.5mm} / {32mm} = 0.12 m$$

On a donc $x=12cm$.

Correction 3

On mesure sur le dessin la distance entre les deux repères et on trouve par exemple $32mm$ ce qui correspond à une distance réelle $$0.50m - 0.20m = 0.30m$$.

On mesure ensuite la distance $d$ entre le repère $0.20m$ et $x$, on trouve $7.5mm$. On effectue un produit en croix.

$$\table \bo \text"plan" , \bo \text"réalité"; 32mm , 0.30m ;7.5mm, d; $$ $$ d = {0.30m × 7.5mm} / {32mm} = 0.07 m$$

Il faut ensuite ajouter cette distance $d$ à la position du repère pour avoir $x$, donc $$ \table x, =, d + 0.20m; , =, 0.07m + 0.20m; ,=, 0.27m; $$

Correction 4

Le principe de résolution est identique à l'exercice 3 en prenant comme distance de référence celle séparant les raies à $541 nm$ et $762nm$.

Première raie

$$\table \bo \text"plan" , \bo \text"réalité"; 24.5mm , 762-541=221nm ;-4.0mm, d_1; $$
$$ d_1 = {-4.0mm × 221nm} / {24.5mm} = -36nm m$$
$$\table λ_1, =, d_1 + 541;, =, -36 + 541; ,=, 505nm ;$$

Deuxième raie

$$\table \bo \text"plan" , \bo \text"réalité"; 24.5mm , 762-541=221nm ;8.0mm, d_1; $$
$$ d_2 = {8.0mm × 221nm} / {24.5mm} = 72nm m$$
$$\table λ_2, =, d_2 + 541;, =, 72 + 541; ,=, 613nm ;$$